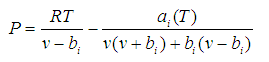 (1)
(1)In 1976, Peng and Robinson proposed a two-constant equation of state, the well-known PR EOS. In 1978, they proposed an improved version of their equation of state for the heavy hydrocarbons. This improved equation is called Predictive Peng-Robinson 78 (PPR78).
For a pure component, the PPR78 EOS is as follows:
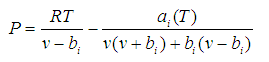 (1)
(1)
Where,
(2)
In the above equations, P is the total pressure, R the ideal gas constant, T the temperature, a and b are EOS parameters, υ the molar volume,TC the critical temperature, PC the critical pressure and ω the acentric factor.
An important feature of the above equation is that the function mi takes two forms depending on the value of the acentric factor. This is a key departure from the 1976 version of the PR model.
For mixtures, the values of a and b are calculated using the classic mixing rules:
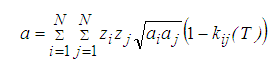 (3)
(3)
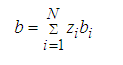 (4)
(4)
Where, zk represents the mole fraction of component k in a mixture, and N the number of components in the mixture. kij(T) is the binary interaction parameter characterizing molecular interactions between molecules i and j. Notice that kij =0 when i = j.
The common practice is to fit the kij(T) so as to represent the vapor-liquid equilibrium data of the mixture under consideration.
For the PPR78 model, the binary interaction parameter kij(T) calculated by group contribution method is given by:
(5)
In the above equation, T is the temperature, ai and bi are calculated in equations (3) and (4), Ng is the number of different groups defined by the method, aik is the fraction of molecule i occupied by group k, and Akl , Bkl are constant parameters allowing the calculation of the binary interaction parameters.
Note that PPR78 uses a group contribution method to estimate the kij(T) parameters. At present, this PPR78 model supports limited groups. See Table 4-11, Chapter 4, Equations of State in the Thermodynamic Data Keyword Manual for more information on this,
The PPR78 model can be used for the prediction of phase equilibria of binary mixtures in both the subcritical and critical regions very accurately. This model uses temperature dependent binary interaction parameter kij to predict the critical locus of the binary systems and the phase behavior of asymmetric systems with high accuracy. In addition to K-values, the PPR78 equation may be used to predict the enthalpies, entropies and densities for the liquid and vapor phases. The predicted liquid phase densities are not very accurate and the API method is selected by default when the PPR78 system is chosen.
Refer "Predictive Peng-Robinson 78 (PPR78)" under "Equations of State" in PRO/II Reference Manual, Chapter 2, Volume 1 for more information.
Limitations
The group interaction parameters in the PPR78 thermo method were obtained through regression of a large collection of experimental equilibrium data supplemented with experimental data for excess enthalpies and excess heat capacity when available. This experiment was performed by Prof. Jean-Nöel Jaubert at the University of Lorraine, France.
PPR78 can provide good estimates of phase behavior within the temperature range represented in the original experimental data that is relevant for the system of interest. The kij predictions are more reliable when excess enthalpy and excess heat capacity data are available for data regression for the system of interest. Excursions away from that temperature range generally also result in good predictions. However, it is known that for some systems the kij estimates at “high” or “low” temperatures largely outside the regressed range can be excessively large in magnitude (say |kij| > 10). Therefore, when using the PPR78 thermo method, users need to pay attention to the simulation results to rule out the possibility of unreasonably large kij values entering the final results.
The evidence of excessively large kij values indicates that for the system in question, either the amount of experimental data was not adequate to generate interaction parameters for reliable kij predictions at the simulation final temperature or the expected phase equilibrium condition was not really feasible at the simulation conditions. An example of the latter is when the physical system of interest generates solids but the simulation tries to model vapor-liquid equilibrium only. The method is provided here without any modifications to the parameters Prof. Jaubert provided. Schneider-Electric does not have the experimental data to perform additional regressions.
Jean-Noel Jaubert; Stephane Vitu; Fabrice Mutelet; Jean Pierre Corriou. Extension of the PPR78 model (predictive 1978, Peng-Robinson ESO with temperature dependent kij calculated through a group contribution method) to systems containing aromatic compounds. Fluid Phase Equilibria . 2005, 237, 193-211.